이진 트리 (Binary Tree)
이진 트리의 종류에 대해서 확실히 모른다는 생각이 들어서 정리해보았다.
- 트리(tree): 노드와 엣지로 이루어진 비선형 계층적 자료구조

이진 트리의 종류
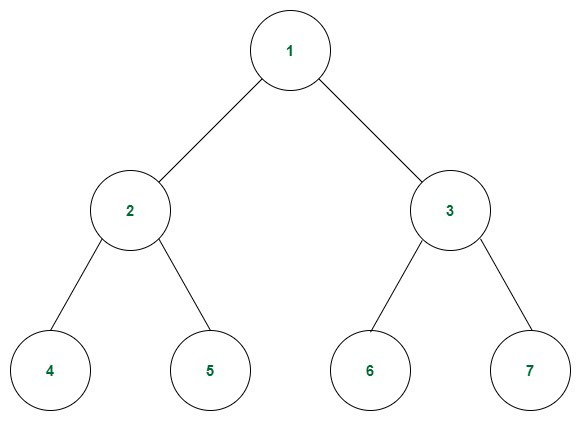
1. 이진 트리: 모든 노드들이 두 개 이하의 자식을 가진 트리

2. 이진 탐색 트리 (Binary Search Tree, BST): 왼쪽 자식은 부모보다 작고 오른쪽 자식은 부모보다 큰 이진 트리

- 삽입, 삭제, 탐색의 시간복잡도: 평균 O(logN), 최악 O(N)
- 순회 종류
- 전위 순회: root -> left child -> right child
- 중위 순회: left child -> root -> right child
- 후위 순회: left child -> right child -> root
3. 정 이진 트리 (full binary tree): 모든 노드가 0개 또는 2개의 자식 노드를 갖는 트리

4. 완전 이진 트리 (complete binary tree): 마지막 레벨 제외하고 모든 레벨이 채워져 있는 트리, 마지막 레벨의 경우 왼쪽부터 채워져 있는 트리

5. 완전 이진 탐색 트리 (complete binary search tree): 완전 이진 트리의 성질을 가지는 이진 탐색 트리
- 완전 이진 트리의 형태를 유지하기 위해 삽입 시 시간이 많이 소요됨
6. 포화 이진 트리 (perfect binary tree): 모든 리프 노드의 레벨이 동일하고 모든 레벨이 가득 채워져 있는 트리
7. 편향 이진 트리 (skewed binary tree): 모든 노드가 왼쪽에 있거나 오른쪽에 있는 트리

8. 균형 이진 트리 (balanced binary tree): 왼쪽과 오른쪽 서브트리의 높이 차이가 모두 1이하만큼 나는 트리
- ex. AVL(높이 균형 이진 탐색 트리), Red-Black 트리
9. 높이 균형 이진 탐색 트리 (AVL): 왼쪽과 오른쪽 자식의 높이 차이가 최대 1까지 차이나는 트리

- 삽입, 삭제, 탐색의 시간복잡도: 평균, 최악 모두 O(logN)
- 트리의 균형을 유지하기 위해 LL-회전, RR-회던, LR-회전, RL-회전이 사용됨
10. Red-Black 트리

- 조건
- 모든 노드는 빨간색 혹은 검은색
- 루트 노드는 검은색
- 모든 NIL(null leaf)는 검은색
- 빨간색 노드의 자식은 검은색
- 모든 리프노드에서 Black Depth는 같다. (리프에서 루트까지의 경로에서의 검은색 노드의 개수가 같음)
- 균형을 더 엄격하게 유지하는 AVL 트리에 비하여 탐색은 분리하지만 삽입, 삭제가 빠름
- 삽입, 삭제, 탐색의 시간복잡도: 평균, 최악 모두 O(logN)
힙(Heap)
최댓값, 최솟값을 찾아내는 연산을 바르게 하기 위해 고안된 완전이진트리

- 최대 힙: 부모 노드의 키 값이 자식 노드의 키 값보다 항상 큰 힙
- 최소 힙: 부모 노드의 키 값이 자식 노드의 키 값보다 항상 작은 힙
자료구조 힙 응용 문제 :: 더 맵게
https://school.programmers.co.kr/learn/courses/30/lessons/42626?language=java
프로그래머스
코드 중심의 개발자 채용. 스택 기반의 포지션 매칭. 프로그래머스의 개발자 맞춤형 프로필을 등록하고, 나와 기술 궁합이 잘 맞는 기업들을 매칭 받으세요.
programmers.co.kr
import java.util.ArrayList;
import java.util.List;
class Solution {
static List<Integer> heap = new ArrayList<>();
public int solution(int[] scoville, int K) {
int answer = 0;
heap.add(-1);
for(int s : scoville){
insert(s);
}
while(true){
int newScovile = delete();
if(newScovile == -1) return -1;
if(newScovile >= K) break;
int nextMin = delete();
if(nextMin == -1) return -1;
newScovile += nextMin*2;
answer++;
insert(newScovile);
}
return answer;
}
public static void insert(int value){
heap.add(value);
int p = heap.size() -1;
while(p > 1 && heap.get(p/2) > heap.get(p)){
int temp = heap.get(p/2);
heap.set(p/2, heap.get(p));
heap.set(p, temp);
p = p/2;
}
}
public static int delete() {
if(heap.size()-1 < 1){
return -1;
}
int deleteItem = heap.get(1);
heap.set(1, heap.get(heap.size()-1));
heap.remove(heap.size()-1);
int p = 1;
while(p*2 < heap.size()){
int minChild = heap.get(p*2);
int minPos = p * 2;
if(p*2+1 < heap.size() && minChild > heap.get(p*2+1)){
minChild = heap.get(p*2+1);
minPos = p*2+1;
}
if(heap.get(p) < minChild) break;
int temp = heap.get(p);
heap.set(p, heap.get(minPos));
heap.set(minPos, temp);
p = minPos;
}
return deleteItem;
}
}- 모든 음식의 스코빌 지수를 하나씩 넣어서 최소힙 구조를 만들어준다.
- 최소힙을 사용하여 루트에 있는 요소(최솟값)를 두 번 연속해서 꺼낸다.
- 꺼낸 값이 K이상이면 최솟값이 K이상이므로 조건을 만족한다. 따라서, break해준다.
- 꺼낼 때 값이 존재하지 않으면 모든 음식의 스코빌 지수를 K이상으로 만들 수 없으므로 -1을 리턴한다.
- 이 두 값을 이용해서 '섞은 음식의 스코필 지수'를 구한 뒤 해당 값을 다시 최소힙에 넣어준다.
'[스파르타코딩클럽] > TIL' 카테고리의 다른 글
| [231221] update 시 Timestamp 값으로 null이 반환 (0) | 2023.12.21 |
|---|---|
| [231219] QueryDSL, JPQL (0) | 2023.12.19 |
| [231213] MySQL 공부 (0) | 2023.12.13 |
| [231211] Spring 심화 개인 과제 피드백 (0) | 2023.12.11 |
| [231207] 심화 주차 조별 과제 (1) | 2023.12.07 |
