728x90
언어 모델(Language Model, LM)
- 언어를 이루는 구성 요소(글자, 형태소, 단어, 단어열 혹은 문장, 문단 등)를 문맥으로 하여 이를 바탕으로 다음 구성 요소를 예측하거나 생성하는 모델
- 예시: 자동완성, 문장생성, 대화시스템, 음성인식, 기계번역, 문서요약
- 통계적 언어 모델(Statistical Language Model, SLM)
- 딥러닝 언어 모델(Deep Neural Network Lanuage Model, DNN LM)
통계적 언어 모델
- 주어진 문서(코퍼스) 내 단어열(혹은 문장)의 등장 확률을 기반으로 각 단어의 조합을 예측하는 전통적인 언어 모델
- 실제로 많이 사용하는 단어열(문장)의 확률 분포를 정확하게 근사하는 것이 모델의 목표
조건부 확률과 언어 모델
- 조건부 확률 P(B|A): 사건 A가 일어났을 때 사건 B가 일어날 확률
- 언어 모델 -> 단어 A가 등장했을 때 바로 다음에 단어 B가 등장할 확률
- 조건부 확률과 결합 확률
- P(A, B) = P(A)P(B|A)
- 연쇄 법칙(Chain rule)
- P(A,B,C,D) = P(A) P(B|A) P(C|A, B) P(D|A,B,C)
- 언어 모델 -> P(나는, 사과를, 먹는다) = P(나는) P(사과를|나는) P(먹는다|나는, 사과를)
- 문제점: 단어가 많아졌을 때 일부 데이터(확률)가 없으면 0이 될 수 있음
- 카운트 기반 계산: 코퍼스(corpus) 내에서 각 단어들의 조합이 나오는 횟수를 카운트한 후 이에 기반하여 확률을 계산
- P(먹는다 | 나는, 사과를) = count(나는, 사과를, 먹는다) / count(나는, 사과를)
- 문제점
- 모든 단어 조합의 경우의 수를 다 세어야 함
- 계산 복잡도가 높아질 뿐만 아니라 무한한 크기의 코퍼스 필요
- 어려움, 비현실적
- 마르코프 가정(Markov assumption)
- 기존 연쇄 법칙의 복잡성을 해결하고 간소화하기 위함
- 미래 사건에 대한 조건부가 과거에 대해서는 독립이며 현재의 사건에만 영향을 받는다는 가정을 전제로 연쇄법칙 설명
- 단어 w_n이 나타날 확률은 그 앞의 단어 w_n-1이 나타날 확률하고만 연관이 있다고 봄
- P(w_1, ... , w_n) = P(w_1) P(w_2|w_1) ... P(w_n|w_n-1)
- 한계
- 언어 현상에 적용하기에는 지나친 단순화
- 언어의 장기 의존성이 간과됨
- 예측 정확도가 낮아질 수 있음
N-gram 언어 모델
- 문장 내 단어는 주변의 여러 단어와 연관된다고 가정
- N: 주변 몇 개의 단어를 볼 것인지 정하는 임의의 숫자
- N-gram: N개의 단어열
- Example: The boy is looking at a pretty girl
- 1-gram(unigram): The, boy, is, looking, at, a, pretty, girl
- 2-gram(bigram): The boy, boy is, ...
- 3-gram(trigram): The boy is, boy is looking, ...
- 4-gram: The boy is looking, ...
- N-1차 마르코프 가정

- 2-gram 모델 예제


- N-gram 성능 비교
- 1-gram 모델의 경우 모든 단어가 독립적이라고 보기 때문에 서로 무관한 단어들이 생성됨
- 2-gram 모델은 1-gram보다 자연스럽지만 전체적으로는 매우 부자연스러움
- 3-gram 모델은 앞보다 자연스럽고 코퍼스에 존재하는 텍스트에 가깝게 생성. 새로운 문장이라고 보기 어려움(low diversity)
- PPL이 낮을 수록 성능이 좋은 모델
- 한계
- 생성된 문장이 지나치게 부자연스럽거나 기존 코퍼스와 지나치게 유사
- 단어열의 확률값이 코퍼스에 따라 크게 달라짐
- 방대한 양의 코퍼스 필요
- 희소성 문제(코퍼스에 등장하지 않는 단어열의 확률값은 모두 0) -> 예측의 정확도를 떨어뜨리는 요인
- 교착어인 한국어에서 희소성 문제가 크게 발생(형태소 분석 등 전처리 진행하지 않으면 조사만 다른 단어가 포함된 단어열의 확률값이 0에 가까워짐)
- 로그 확률(Log probabilities)
- 언어 모델의 확률 계산 시 원래 확률값에 로그(log)를 취하는 것이 보편적
- 이는 언더플로(underflow)를 피하기 위함
- 곱셈 연산은 계산 리소스가 크고 결과값이 0에 가까워짐 -> 로그 공간에서 계산할 시 덧셈으로 환산 -> 계산이 간단해지고 언더플로를 피할 수 있음

일반화(Generalization)
- 통계적 언어 모델은 제한된 양의 코퍼스로 인해 새로운 단어열에 대해서는 제대로 예측하지 못하고 정확도가 떨어짐
- 이와 같은 희소성 문제를 해결하고 모델의 일반화 능력을 향상시키기 위해 다양한 일반화 기법들이 제시됨
1. 스무딩(Smoothing)
- 모델이 한 번도 본 적없는 단어 조합(unsen n-gram)에 특정 값(α)을 부여하여 확률 분포에 약간의 변화를 주는 방법 (0 < α ≤1)
- 코퍼스에 없는 단어열로 인해 전체 문장의 확률이 0이 되는 희소성 문제 방지

- 라플라스 스무딩(Laplace smoothing): α=1로 지정. 최소 한 번은 등장했다고 가정.
- 제로 데이터(코퍼스에 등장하지 않는 단어열)가 적은 경우 유용
- 그러나 단어의 빈도수에서 크게 벗어나는 문제를 야기
- N-gram 모델의 일반화 문제는 완전히 해소되지 않음
2. 보간법(Interpolation)
- 특정 N-gram의 확률을 이전 N-gram의 확률과 섞는 방법
- 3-gram 모델 예시: 2-gram, 1-gram 모델의 확률까지 모두 구한 후 일정한 비율(λ)의 가중치를 각각 곱한 후 모두 합하는 방식 (0 < λ ≤1, ∑λ_i = 1)
- 제로 데이터들의 N-gram 정보에 따라 서로 다른 빈도를 부여할 수 있음
- 단점: 가중치를 얼마나 부여할 것인지?

3. 백오프(Back off)
- 보간법과 같이 여러 N-gram을 함께 고려하지만 모든 N-gram의 확률을 합하지 않는다는 점이 차이
- 1-gram ~ N-gram 확률 중 빈도수가 0이상이며 N의 차수가 높은 N-gram 확률을 사용

생각해볼 문제: 사람의 일반화와 차이점
- 일반화 방법은 문장 내에서 유사한 패턴을 찾음으로써 새로운 정보를 학습하는 사람의 일반화 방식과는 사뭇 다름
- 훌륭한 언어 모델이라면 문장 내에 처음 보는 단어 혹은 단어열이 있다고 하더라도 문장 내 단어열 간의 유사도(패턴)를 고려하여 새로운 단어열에 대해 추론할 수 있는 일반화가 가능해야 함
- 딥러닝 언어 모델에서의 주요 과제 중 하나
모델 평가와 퍼플렉서티(Perplexity)
- 언어 모델의 평가: 일반적인 방법은 모델 간 비교. 하지만 상당한 시간 소요.
- 퍼플렉서티(Perplexity, PPL): 언어 모델의 성능을 자체적으로 평가하는 내부 평가 척도
- 간이 실험 등 짧은 시간 안에 간단히 모델을 평가할 때, 혹은 모델 간 비교시 평가 척도로 사용
- 'perplexity'는 '헷갈리는 정도'를 뜻함
- 모델이 선택할 수 있는 경우의 수를 의미하는 분기계수 (branching factor)
- 즉, 얼마나 많은 후보군을 두고 고민하는가를 나타냄
- 모델이 데이터셋에 대하여 확률 분포를 얼마나 확실하게 (헷갈리지 않게) 예측할 수 있는지를 나타내는 지표
- PPL 점수가 낮을 수록 (헷갈리는 경우가 적을수록) 좋음
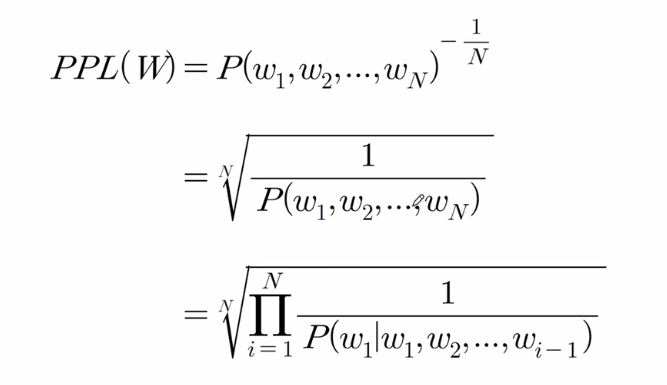
'대학공부 > 자연어처리' 카테고리의 다른 글
| 자연어처리 task (0) | 2024.03.27 |
|---|---|
| 자연어 분석 (0) | 2024.03.20 |
| 자연어처리의 기본 (2) | 2024.03.13 |
| 인간 지능을 흉내 내는 인공지능 (0) | 2024.03.13 |



