1. K-평균 군집화와 퍼지 군집화
- K-Means Clustering
- 사전에 군집의 개수 K를 결정
- 각 군집에는 중심이 존재하게 되는데, 중심과 군집 내 데이터 거리 차의 제곱 합을 최소로 하는 최적 군집을 찾음
- 일단 중심 K개를 찍고 반복
- Python에서의 K-평균 군집화
# 알고리즘 수행을 위해 필요한 라이브러리
import matplotlib.pyplot as plt
import pandas as pd
from sklearn.cluster import KMeans
plt.figure(figsize = (10, 5))
# K-means Clustering의 실제
df = pd.read_csv('menu.csv', engine = 'python')
df_data = df[['가격', '판매량']] # 군집화하기 위해 사용할 데이터
km = KMeans(n_clusters = 4, random_state = 0)
km.fit(df_data)
result = km.predict(df_data)
# result 출력
array([0, 0, 0, 2, 2, 1, 1, 3, 0, 2, 0, 3, 3, 2, 3, 2, 3, 2, 1, 3, 2, 1,
0, 0], dtype=int32)
# 군집의 중심 위치를 출력
km.cluster_centers_
"""
array([[ 6471.42857143, 43697.85714286],
[ 6275. , 73505.5 ],
[ 6085.71428571, 55502.57142857],
[ 5316.66666667, 82752.83333333]])
"""
# 할당 결과를 DataFrame에 추가
df['CLUSTER'] = result
# scatterplot 형식으로 시각화
plt.scatter(df['가격'], df['판매량'], c = df['CLUSTER'])
plt.show

가격과 판매량의 scale의 차이로 인해 가격 속성이 등한시 됨 -> 스케일링 필요
EXERCISE 1

- 1번
- 중심점 C에 속하는 군집: C, F, G -> 평균: (7, 15)
- 중심점 E에 속하는 군집: A, B, D, E, H -> 평균: (5, 8)
- 2번
- 중심점 (7, 15)에 속하는 군집: C, F, G, H -> 평균: (7, 14)
- 중심점 (5, 8)에 속하는 군집: A, B, D, E -> 평균: (5, 8)
중심점: (7, 14), (5, 8)
일반적으로 적은 연산으로 빠르다는 특징
군집 개수 K를 정하는 방법
- Elbow Method
- 가로축을 K, 세로축을 오차로 하는 그래프에서 기울기가 완만해지는 지점을 최적의 K로 선택
- 팔꿈치에 해당하는 점

각각의 데이터가 한 군집에 할당되어야 할까?
- Fuzzy Clustering(퍼지 군집화)
- K-평균 군집화 등 다수의 군집화 방법론은 단일 데이터에 대해 반드시 하나의 군집만 할당한다는 특성을 지님
- 각각의 데이터마다 특정 군집에 속하게 될 가중치를 배정하는 방식
- FCM 알고리즘(Fuzzy C-Means Algorithm)
- 대표적인 퍼지 군집화
- 사전에 정의된 퍼지 승수 p와 군집 수 K에 대해 다음과 같은 절차로 군집화를 수행
- 개별 데이터에 대해 임의로 각 군집에 속하게 될 가중치를 부여
- 부여된 가중치를 이용하여 각 군집의 중심이 어디인지 계산
- 군집 별 중심에 부합하게끔 개별 데이터에 대한 가중치 재계산
- 재계산된 가중치에 기초하여 새로운 군집 별 중심 계산
- 가중치가 일정한 값에 수렴할 때까지 가중치 재계산과 군집 중심 재계산 반복
- 개별 데이터들의 가중치를 알 때 군집의 중심을 계산하는 방법은?
- 퍼지 승수 p: 1~∞, 보통 2 -> 가중치마다 (가중치)^p

군집 A 중심 (x1, x2)
x1 = (-300 * 0.04 - 200 * 0.09 + 200 * 0.25 + 100 * 0.16) / (0.04 + 0.09 + 0.25 + 0.16) = 19.44
2. 밀도 기반 군집화와 DBSCAN
- K-평균의 한계

- 여러 가지 군집화 방법론
- K-means
- 군집의 수를 정해 놓고, 각 군집의 중심에 데이터가 최대한 몰리게끔 군집화
- 원형으로 몰려 있는 데이터가 아닌 경우 부적절하다는 단점
- 밀도 기반 군집
- 같은 군집에 속한 데이터들은 끼리끼리 밀도 있게 모여 있을 것이라 가정
- Density-Based Spatial Clustering of Applications with Noise (DBSCAN)
- 계층적 군집화
- 유사도가 높은 개체끼리 묶고, 그 군집을 다시 다른 개체와 묶는 과정을 반복
- Dendrogram을 통해 군집화 결과를 시각화할 수 있음
- K-means
- DBSCAN
- 원의 반지름과 원 안에 포함될 최소 점 개수를 사전에 지정
- 최조 개수보다 더 많은 점이 포함되면 원으로 점들을 묶음
- 만들어진 원들을 하나로 이어 최종 군집을 결정
- 군집에 포함되지 않은 점을 Noise(이상치)라고 함

- Python과 DBSCAN
# 군집화 및 시각화를 위한 라이브러리 불러오기
import pandas as pd
from sklearn.cluster import DBSCAN
import matplotlib.pyplot as plt
# csv 파일을 불러와 데이터프레임에 저장
df = pd.read_csv('housing.csv')
house_position = df[['x', 'y']]
# 모수 결정 및 DBSCAN 군집화 수행
db = DBSCAN(eps = 10, min_samples = 3)
cluster_pred = db.fit_predict(house_position)
# 원본 데이터가 어떤 군집에 속하게 되었는지 확인
df['CLUSTER'] = cluster_pred
# 군집화 결과 시각화
x = house_position['x']
y = house_position['y']
plt.scatter(x, y, c = cluster_pred)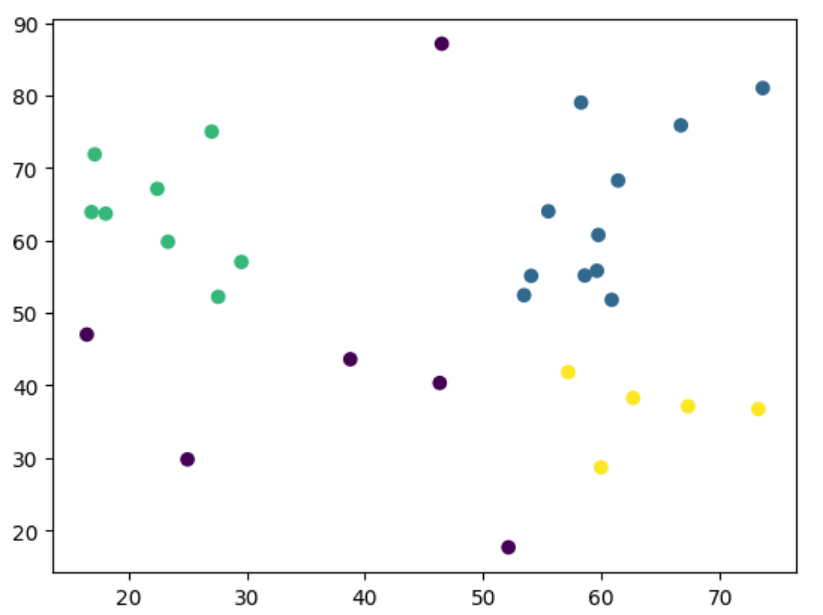
- Hierarchical DBSCAN
- 계층적 차원에서 DBSCAN을 수행함으로써 종전 방법론의 문제점을 개선
- 반경에 해당하는 epsilon 값을 설정하지 않아도 군집화가 가능
- 군집간 밀도 차로 인해 군집화가 잘못된 방향으로 이루어지는 문제를 해결
EXERCISE 2

ㄱ. O -> (B)에서 원이 작아지기 때문에 다른 군집에 속하게 될 수 있음
ㄴ. O -> (C)에서 원이 커지고 min_samples의 개수가 적어지므로 군집에 더 많은 데이터가 속할 수 있음
ㄷ. X -> (A)에서 min_samples의 개수가 늘어나므로 노이즈로 분류되었다면 마찬가지로 노이즈임
3. Dendrogram과 계층적 군집화
- Hierarchical Clustering(계층적 군집화)
- 데이터로 주어진 모든 개체끼리의 유사도를 계산
- 유사도가 가장 높은 두 개체를 하나의 군집으로 묶음
- 같은 과정을 반복해 Tree 형태로 최종 군집화 수행
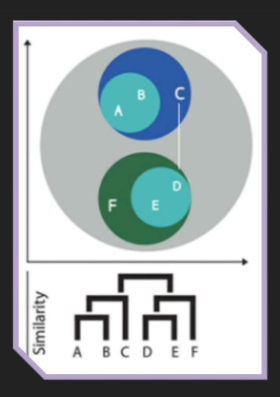
- 군집간 유사도 계산 방법
- Sigle Linkage: 서로 다른 그룹의 점 사이 거리의 최솟값
- Complete Linkage: 서로 다른 그룹의 점 사이 거리의 최댓값
- Average Linkage: 서로 다른 그룹의 점 사이 거리의 평균값
- Centroid Linkage: 각 그룹의 중심을 계산하여 중심간 거리
- Ward Linakage: 그룹끼리 합칠 시 늘어날 오차 제곱 합(SSE)을 최소화하는 방향으로 군집화를 수행
- 계층적 군집화, Python으로
# 계층적 군집화 및 시각화를 위한 라이브러리 불러오기
import pandas as pd
import matplotlib.pyplot as plt
import scipy.cluster.hierarchy
from scipy.cluster.hierarchy import linkage
from scipy.cluster.hierarchy import dendrogram
# 주택 데이터 불러오기 및 계층적 군집화 수행
df = pd.read_csv('housing.csv')
house_position = df[['x', 'y']]
linked = linkage(house_position, 'single')
dendrogram(linked, orientation = 'top')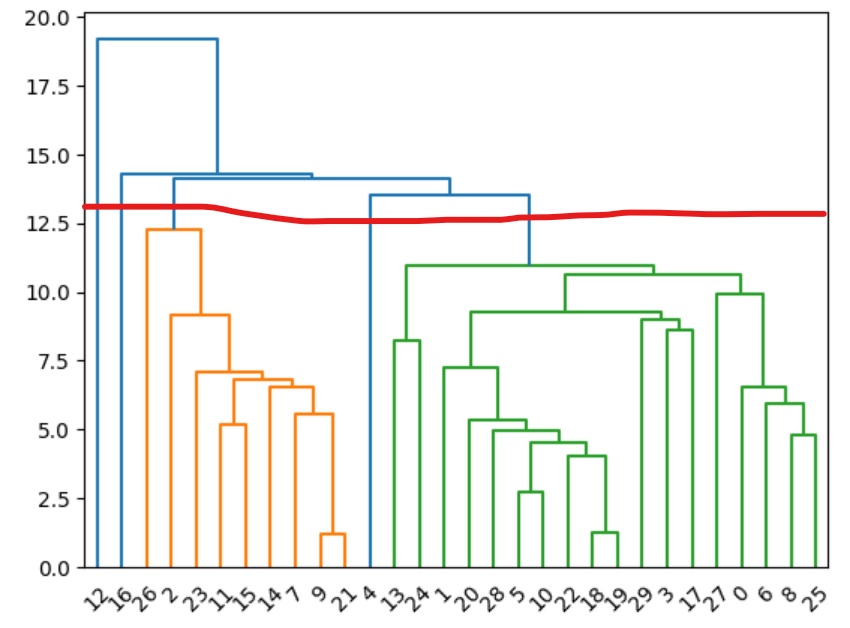
빨간 선을 기준으로 군집화하는 경우: (12), (16), (26, 2, 23, ..., 21), (4), (13, 24, 1, ..., 25)
그래서 어떤 방법이 제일인가?
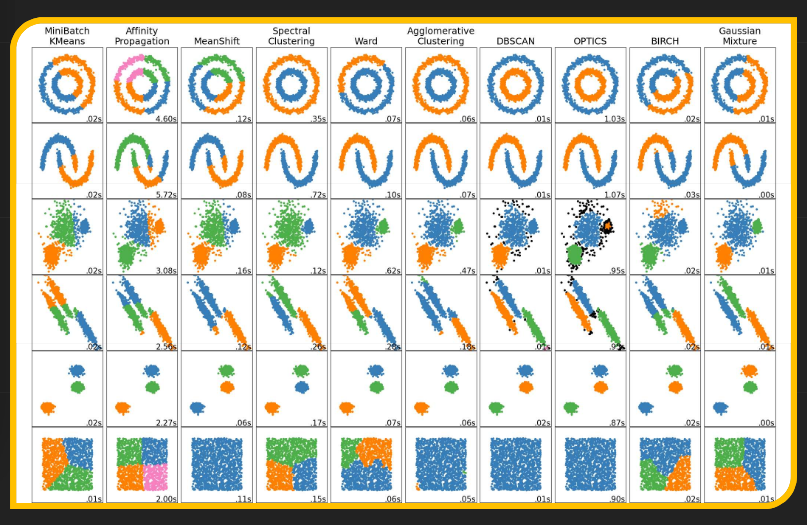
4. 군집화 결과에 대한 평가
- 실루엣 기법(Silhouette Analysis)
- 군집화를 모두 마친 이후, 모든 데이터에 대하여 실루엣 계수를 계산 후 도식화
- 실루엣 계수의 범위는 -1 이상 1 이하이나 음수인 경우는 드묾
- 실루엣 계수의 값이 클수록 군집화가 더 잘 이루어진 것임
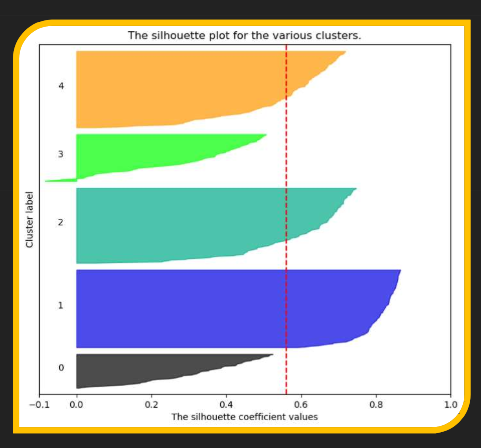
- 실루엣 계수 계산 방법
- A: 최근접 군집과의 평균 거리(다른 군집에 해당하는 모든 데이터들과의 거리 평균 중 가장 작은 값)
- B: 할당된 군집과의 평균 거리(같은 군집에 해당하는 모든 데이터들과의 거리 평균)
- 실루엣 계수: (A - B) / max(A, B)
- Hopkins Statistic
- 군집화 수행 이전, 해당 데이터셋이 군집화하기에 적절한지 판단하기 위한 지표
- 값의 범위: 0 이상 1 이하 (1에 가까울 수록 군집화하기에 좋음)
- 주어진 데이터셋에서 N개의 표본을 추출
- (전체 데이터셋 범위에서) 균등분포에서 무작위 N개의 표본을 추출
- 모든 표본에 대해 최근접 데이터와 거리 계산
- 아래의 식이 홉킨스 통계량
- H = (균등분포 표본 거리 합) / {(균등분포 표본 거리 합) + (데이터셋 표본 거리 합)}
'대학공부 > 데이터과학' 카테고리의 다른 글
| 데이터 거버넌스와 데이터과학의 미래 (0) | 2024.05.27 |
|---|---|
| 연관규칙 생성과 연관분석의 실제 (0) | 2024.05.13 |
| 여러 가지 방법을 이용한 분류 (0) | 2024.04.29 |
| 개인정보 비식별화와 데이터 윤리 (0) | 2024.04.08 |
| 의사결정나무를 이용한 분류와 예측 (1) | 2024.04.01 |