- 기본 용어
- 부울 대수: 논리 연산자(AND, OR, NOT)을 사용하여 논리적 기능을 처리하는 논리 수학
- 부울식: 논리적 기능을 기호로 나타낸 식
- 논리 변수: 시간에 따라 변하는 논리 치를 갖는 양
- 논리 연산자: 논리 시스템을 해석하고 설계하는데 사용되는 기본적인 기능
- 논리 함수: 임의의 시스템을 갖고 있는 논리적인 기능
- 진리표: 모든 가능한 경우의 논리적인 입력과 출력과의 관계를 나타낸 표
- 부울 수위칭 대수

- 부울 함수
- Closure: 연산자 +, · (or, and)
- 단위원(indentity element): 0, 1 -> 0+x=x, 1·x=x
- 교환성(commutative law): x+y = y+x, x·y=y·x
- 분배성(distributive law): x·(y+x) = (x·y)+(x·z)
- 보수: x+x'=1, x·x'=0
- 쌍대(Duality): 상수 0과 1을 서로 바꾸고, and와 or 연산을 서로 바꾼 것

Example. 다음 부울 함수가 리터럴의 개수가 최소가 되도록 간략화하라.
1. x(x' + y) = xx' + xy = 0+ xy = xy
2. x + x'y = x + xy +x'y = x + y(x + x') = x + y
3. (x + y)(x + y') = x + xy' + xy + 0 = x (1 + y + y') = x
4. xy + x'z + yz = xy + x'z + yz(x + x') = xy(1 + z) + x'z(1 + y) = xy + x'z
5. (x + y)(x' + z)(y + z) = (0 + xz + x'y + yz)(y + z) = xyz + xz + x'y + x'yz + yz + yz
= z(xy + x + x'y +y) + x'y = z[y(x + x')+ x + y] + x'y = z(x + y) + x'y = xz + yz + x'y
*** 5번은 4번의 쌍대 이므로 4번 답의 쌍대를 구하면됨! (x+y)(x'+z) = xz + yz + z'y
- 함수의 보수: (A + B + C + D + ... + F)' = A' + B' + C' + D' + ... + F'
Example 1. 함수 F1 = x'yz' + x'y'z와 F2 = x(y'z' + yz)의 보수를 구하라.
F1' = (x'yz' + x'y'z)' = (x'yz')'(x'y'z)' = (x+y'+z)(x+y+z')
F2' = [x(y'z' + yz)]' = x' + (y'z' + yz)' = x' + (y'z')'(yz)' = x' + (y+z)(y'+z')
Example 2. 위 함수 F1, F2의 쌍대를 취하고 각 리터럴을 보수화하므로써 F1과 F2의 보수를 구하라.
F1의 쌍대 = (x'+y+z')(x'+y'+z) -> (x+y'+z)(x+y+z') = F1'
F2의 쌍대 = x+(y'+z')(y+z) -> x'+(y+z)(y'+z') = F2
- Canonical Forms
- Minterm(최소항): 이진 변수에 대한 AND의 항(표준 곱)
- Maxterm(최대항): 이진 변수에 대한 OR의 항(표준 합)
- 둘은 보수 관계


-> 최소항으로 나타낼 때 결과가 1이 되는 변수들의 곱을 다 더해줌
-> 최대항으로 나타낼 때 결과가 0이 되는 변수들의 합을 다 곱해줌
- Sum of Minterm(최소항의 합)
- 부울함수의 변수들이 모두 and로 붙어있어야 함! 따라서 없는 변수 x를 (x+x') 모두 곱해준다.

- Product of Maxterm(최대항의 곱)
- F = xy + x'z
- F' = (x+y)(x'+z) = xz + x'y + yz = xz(y+y') + x'y(z+z') + yz(x+x')
- = xyz + xy'z + x'yz + x'yz' + xyz + x'yz = xyz + xy'z + x'yz + x'yz'
- (F')' = (x+y+z)(x+y'+z)(x'+y+z)(x'+y+z') = M0M2M4M5 = ∏(0, 2, 4, 5)
- Conversion between Canonical Forms
- F(x, y, z) = Σ(1, 3, 6, 7) = ∏(0, 2, 4, 5)
- Standard Forms
- Sum of product(SOP): F1 = y' + xy + x'yz
- Product of sum(POS): F2 = x(y'+z)(x'+y+z'+w)
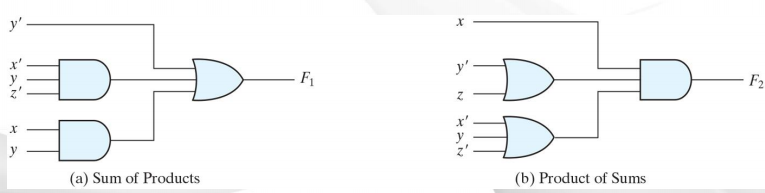
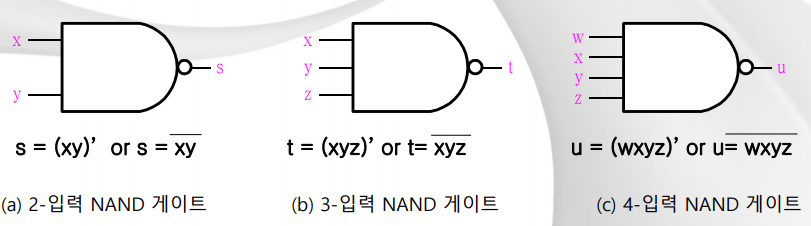
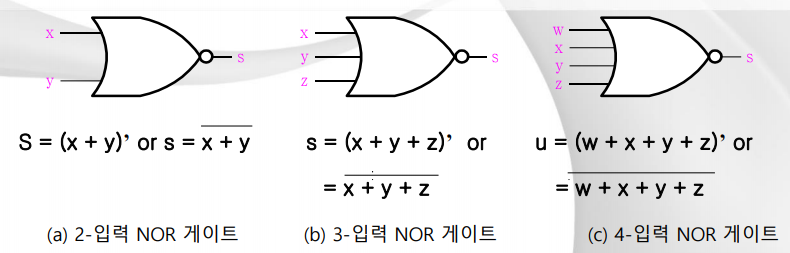
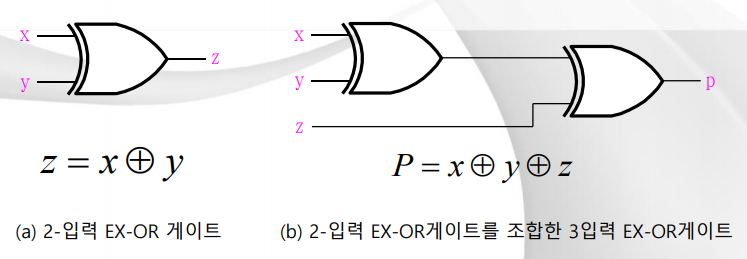
- 2진 논리함수
1. AND 게이트의 논리 기호

2. OR 게이트의 논리 기호

3. NOT 게이트의 논리 기호

4. NAND 게이트의 논리 기호
5. NOR 게이트의 논리 기호
6. EX-OR 게이트의 논리 기호
7. EX-NOR 게이트의 논리 기호

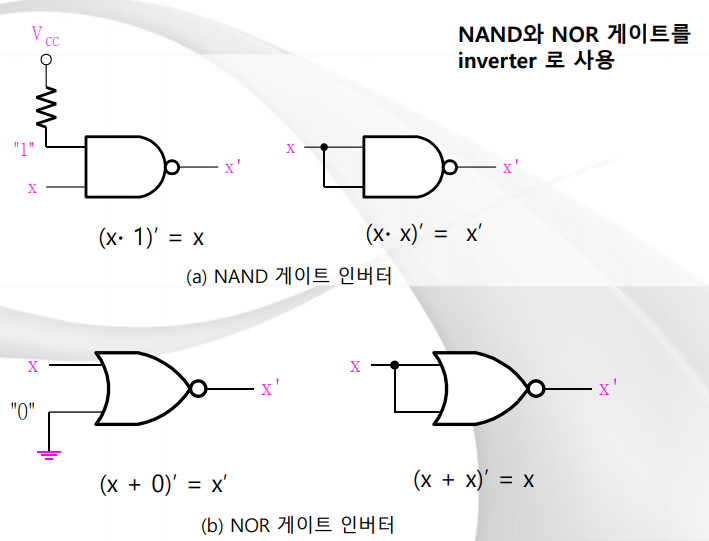
- NAND와 NOR 게이트를 inverter로 사용
- NAND 게이트를 사용한 AND와 OR 함수

'대학공부 > 논리설계' 카테고리의 다른 글
| 03. 게이트 레벨 최소화(Minimization) (0) | 2023.09.09 |
|---|---|
| 01. 디지털 시스템과 2진수 체계 (0) | 2023.09.09 |