03. 게이트 레벨 최소화(Minimization)

• DeMorgan
  • 부울 대수의 중요 부분인 두 가지의 정리를 제안한 논리 학자이며 수학자

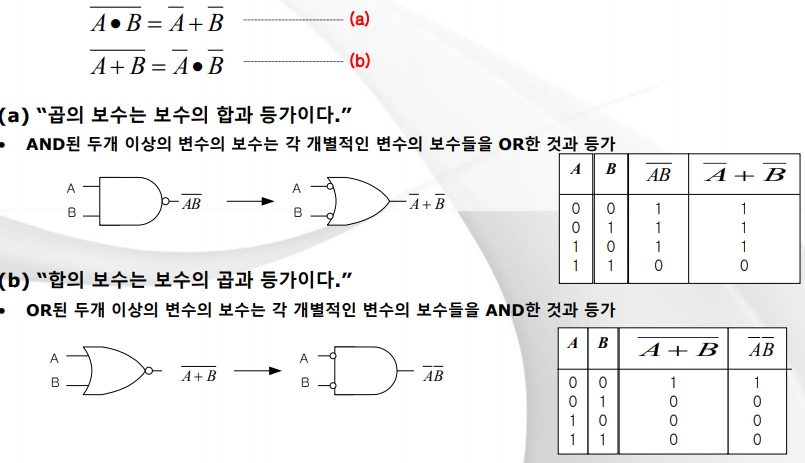
• DeMorgan 정리

 

• 게이트 레벨 최소화(Minimization)
  • 부울 함수의 최적의 게이트 레벨 구현을 위한 설계 최소화 작업
  • 진리표 -> Karnaugh Map (K-map)
  • 부울 식에서 최대항과 최소항을 표현하는 사각행렬

 

• Map 방법

1. 변수 2개

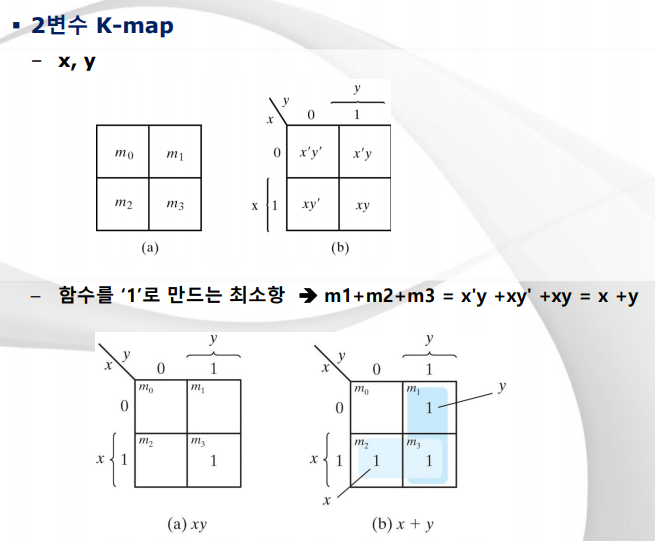
      * a + bc = (a+b)(a+c)이므로 x'y + x(y+y') = x'y + x = (x+x')(x+y) = x+y

 

2. 변수 3개

 

d

• Map을 이용한 부울대수 간략화: 최대 직사각형으로 묶어줌

3. 변수 4개

• Map을 이용한 부울대수 간략화

4. 변수 5개

 

• Don't care condition
  • 함수에 따라서 절대 발생되지 않는 입력 조건의 존재가 가능
  • 논리회로의 동작에 아무런 영향을 미치지 않음 -> 무정(무관)의 조건
  • 규정되지 않은 최소항들에 대하여 0이 되든 1이 되든 상관없음
  • 맵 안에서 함수를 단순화 하기 위하여 사용 - X로 표시, X를 포함한 최대 직사각형 찾기
• Karnaugh map 특징
  • 장점
    1. 그림으로 복잡한 부울 함수 간소화 가능
    2. 복잡한 수식이나 공식을 몰라도 간소화 가능
    3. 간소화된 결과를 손쉽게 확인 가능
  • 단점
    1. 변수가 6개 이상이면 그리기 어려움
    2. 프로그램화 하기 어려움
    3. 모든 경우를 설계자가 간소화 해야 함 (설계자에 따라 간소화된 결과가 다름)

 

• AND와 OR을 NAND와 NOR로 구현

 

• XOR
  • x ⊕ y = xy' + x'y
  • (x ⊕ y)' = xy + x'y'
  • x ⊕ 0 = x
  • x ⊕ 1 = x'
  • x ⊕ x = 0
  • x ⊕ x' = 1
  • x ⊕ y' = x' ⊕ y = (x ⊕ y)'

• Parity Generation and Checking