실습 2차시: DT

*Colab 이용

!pip install mglearn

지니 불순도 (Gini Impurity)

 

지니 불순도는 결정 트리의 분할기준 중 하나입니다.

아래 두개의 트리를 살펴봅시다.

 

 

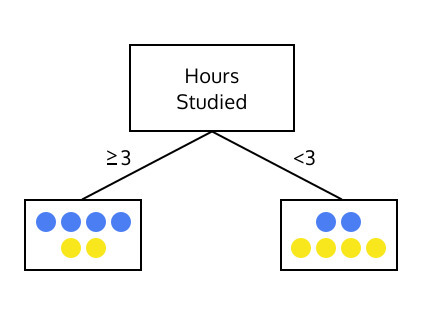
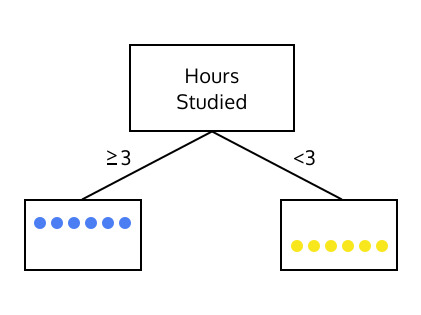
둘 중 어느 트리가 학생이 성적을 더 높게 받을 수 있을지 예측하는데 유용할까요?

이 질문은 한 세트의 instance 들에 대해 지니 불순도 를 계산함으로써 답할 수 있습니다.

지니 불순도를 찾기 위해서는 1에서 시작해서 세트의 각 class 비율의 제곱을 빼면 됩니다.

 

Gini Impurity=1−Gini Index=1−∑pi^2 (i=1 ~ K)

위 식에서 K은 class label의 개수이며, pi은 i번째 class label의 비율입니다.

예를 들어, A class인 instance가 3개 있고 B class인 instance가 1개 있는 데이터의 경우에는 지니 불순도는 아래와 같이 계산됩니다.

1−(3/4)^2−(1/4)^2=0.375

만약 데이터가 하나의 class만 있다면, 지니 불순도는 0이 됩니다. 불순도가 낮으면 낮을수록 결정 트리의 성능은 더 좋아집니다.

# 위 그림의 왼쪽 결정트리의, 왼쪽 끝마디 노드의 지니 불순도를 계산해봅시다.

1 - (4/6)**2 - (2/6)**2

0.4444444444444445

 

 

아래의 sample_labels 리스트의 지니 불순도를 계산해봅니다.

sample_labels = ["unacc", "unacc", "acc", "acc", "good", "good"]

impurity = 1

1. 이제 sample labels에 포함되어있는 class가 각 몇개씩 들어있는지 세어봅니다.

from collections import Counter

label_counts = Counter(sample_labels)

print(label_counts)

Counter({'unacc': 2, 'acc': 2, 'good': 2})

 

2. 데이터셋에서 각 label의 확률을 계산해봅니다.

for label in label_counts:

  print(label)

  probability_of_label = label_counts[label] / len(sample_labels)

  print(probability_of_label)

unacc

0.3333333333333333

acc

0.3333333333333333

good

0.3333333333333333

 

3. 그리고 그 확률을 이용하여 sample_labels의 불순도를 계산해봅니다.

for label in label_counts:

  #print(label)

  probability_of_label = label_counts[label] / len(sample_labels)

  impurity -= probability_of_label**2

  #print(probability_of_label)

print(impurity)

0.6666666666666665

 

4. 지니 불순도를 계산하는 함수로 만듭니다.

def gini(dataset):

  impurity = 1

  label_counts = Counter(dataset)

  for label in label_counts:

    prob_of_label = label_counts[label] / len(dataset)

    impurity -= prob_of_label**2

  return impurity

 

---

정보증가량 (Information Gain)

이제 지니 불순도가 leaf node를 만들기 위해서 어떠한 feature에 따라 데이터를 나누어야하는지 결정해야 합니다.

예를 들어, 학생들의 수면 시간 또는 학생들의 공부 시간 둘 중 어느 feature을 기준으로 학생들을 나누어야 더 좋은 tree를 만들 수 있을까요?

위 질문에 답하기 위해 어떠한 feature에 대하여 데이터를 나누었을 때의 정보증가량을 계산해야 합니다.

정보증가량은 데이터 분할 전과 후의 불순도 차이를 측정합니다.

예를 들어, 불순도가 0.5인 데이터를 어떠한 feature에 대해 나누었을 때, 불순도가 각각 0, 0.375, 0 인 끝마디가 생긴다고 가정해봅니다.

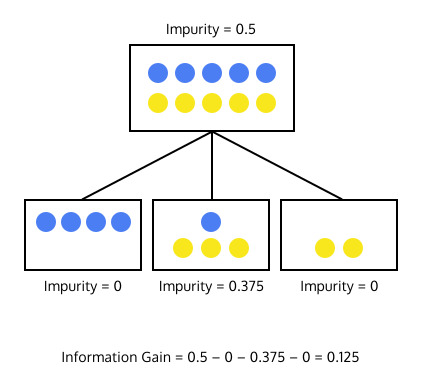
이 경우에 데이터를 나누는 정보증가량은 0.5 - 0 - 0.375 - 0 = 0.125 입니다.

데이터를 나누었을때의 정보 증가량은 양수입니다. 따라서, 위처럼 결정 지점을 나눈 것은 결과적으로 불순도를 낮추었기 때문에 좋은 결정 지점입니다. 정보증가량은 크면 클수록 좋습니다.

 

아래는 unsplit_labels라는 임의의 데이터입니다. unsplit_labels을 두가지 다른 분할 지점으로 나누었습니다.

이는 split_labels_1와 split_labels_2 입니다. 각 분할에 대해 information gain을 계산해봅니다.

unsplit_labels = ["unacc", "unacc", "unacc", "unacc", "unacc", "unacc", "good",

                  "good", "good", "good", "vgood", "vgood", "vgood"]

split_labels_1 = [["unacc", "unacc", "unacc", "unacc", "unacc", "unacc", "good", "good", "vgood"],

                  [ "good", "good"],

                  ["vgood", "vgood"]]

split_labels_2 = [["unacc", "unacc", "unacc", "unacc","unacc", "unacc", "good", "good", "good", "good"],

                  ["vgood", "vgood", "vgood"]]

# unsplit_labels의 지니 불순도를 계산해봅니다.

info_gain_1 = gini(unsplit_labels)

info_gain_1

0.6390532544378698

 

1. split_labels_1의 각 부분집합에 대하여 지니 불순도을 계산하여 정보 증가량을 계산해봅니다.

for subset in split_labels_1:

  info_gain_1 -= gini(subset)

print(info_gain_1)

0.14522609394404257

 

2. split_labels_2에 대해서도 동일한 방법으로 정보증가량을 계산해봅니다.

info_gain_2 = gini(unsplit_labels)

for subset in split_labels_2:

  info_gain_2 -= gini(subset)

print(info_gain_2)

0.15905325443786977

 

3. 정보증가량을 계산하는 함수를 만들어봅니다.

def information_gain(starting_labels, split_labels):

  info_gain = gini(starting_labels)

  for subset in split_labels:

    info_gain -= gini(subset)

  return info_gain

 

---

가중 정보증가량 (Weighted Information Gain)

만약 정보증가량이 0이라면 그 feature에 대해 데이터를 나누는 것은 소용이 없습니다. 때에 따라서 데이터를 나누었을 때 정보증가량이 음수가 될 수 있습니다. 이 문제를 해결하기 위해서 가중 정보증가량 (weighted information gain)을 사용합니다.

분할 후에 생성되는 데이터의 부분집합의 크기 또한 중요합니다. 예를 들어서, 아래 이미지에서는 불순도가 같은 두 부분집합이 있습니다.

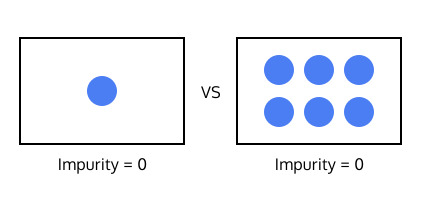
어느 부분집합을 결정 트리의 끝마디로 정하는게 좋은 결정트리를 만들 수 있을까요?

두 부분집합은 모두 불순도가 0으로써 완전하지만, 두 번째 부분집합이 더욱 의미있습니다. 두 번째 부분집합에는 많은 개수의 instance들이 있기 때문에 이 부분집합이 구성된 것이 우연이 아님을 알수 있습니다.

그 반대를 생각해보는 것도 도움이 됩니다. 아래 그림에서 같은 값의 불순도를 가지고 있는 두 부분집합이 있습니다.

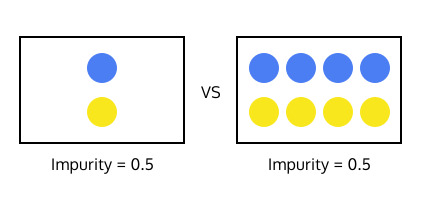
이 두 부분집합의 불순도는 굉장히 높습니다. 그렇지만 어느 부분집합의 불순도가 더 큰 의미를 가질까요? 왼쪽의 부분집합을 분할하는 것보다는 오른쪽 부분집합을 분할하여 불순도가 없는 집합을 만드는 것이 정보증가량이 더 클 것입니다. 따라서, 집합의 instance 개수를 고려하여 정보증가량을 계산해야 합니다.

집합의 크기까지 고려하도록 정보증가량 함수를 수정할 것 입니다. 단순히 불순도를 빼는 것에서 더 나아가 분할된 부분집합의 가중 불순도를 뺄 것입니다. 만약 분할 전의 데이터가 10개의 instance을 가지고 있고 하나의 부분집합이 2개의 instance가 있다면, 그 부분집합의 가중 불순도는 2/10 * impurity가 되어 instance 숫자가 적은 세트의 중요도를 낮춥니다.

가중 정보증가량 계산의 예시는 아래와 같습니다.

 

 

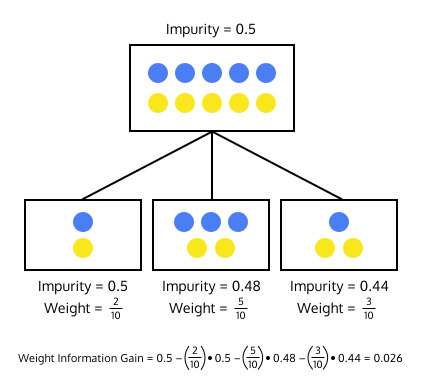
이번 활동에서 사용할 데이터는 Car Data Set입니다. 아래는 데이터셋의 각 feature와 class label에 대한 설명입니다.

Car dataset은 class에 해당하는 4가지 label과 각 차량의 특징을 나타내는 6개의 feature을 갖고 있습니다.

Label은 4개의 class - unacc(unacceptable), acc(acceptable), good, vgood로 이루어져 있으며, 각 class는 차량 구매시의 만족도(acceptability)를 나타냅니다.

각 차량은 6개의 feature을 가지고 있고, 아래와 같습니다.

• buying (차량의 가격): "vhigh","high","med", or "low".
• maint (차량 유지 비용): "vhigh","high","med", or "low".
• doors (차의 문 갯수): "2","3","4","5more".
• persons (차량의 최대 탑승 인원): "2","4", or "more".
• lug_boot (차량 트렁크의 사이즈): "small","med", or "big"
• safety (차량의 안전성 등급): "low","med", or "high".

# 샘플 데이터

cars = [['med', 'low', '3', '4', 'med', 'med'],

        ['med', 'vhigh', '4', 'more', 'small', 'high'],

        ['high', 'med', '3', '2', 'med', 'low'],

        ['med', 'low', '4', '4', 'med', 'low'],

        ['med', 'low', '5more', '2', 'big', 'med'],

        ['med', 'med', '2', 'more', 'big', 'high'],

        ['med', 'med', '2', 'more', 'med', 'med'],

        ['vhigh', 'vhigh', '2', '2', 'med', 'low'],

        ['high', 'med', '4', '2', 'big', 'low'],

        ['low', 'low', '2', '4', 'big', 'med']]

car_labels = ['acc', 'acc', 'unacc', 'unacc', 'unacc', 'vgood', 'acc', 'unacc', 'unacc', 'good']

1. information_gain 함수를 수정하여 가중 정보증가량을 계산해보도록 합니다. 새로운 함수의 이름은 weighted_information_gain 입니다.

가중치: 부분집합의 label 갯수 len(subset) / 분할 전의 집합의 label 갯수 len(starting_labels)

def weighted_information_gain(starting_labels, split_labels):

  info_gain = gini(starting_labels)

  for subset in split_labels:

    info_gain -= gini(subset) * (len(subset) / len(starting_labels))

  return info_gain

• 파이썬 문법 참고
  • List comprehension 기법: 리스트명 = [ 표현식 for 변수 in 반복 가능한 대상 if 조건문 ]
  • Set 자료형: 중복을 제거하기 위한 필터 역할로 사용하기도 함

2. 아래 split() 함수를 살펴보겠습니다.  ->  지정한 column에 따라 데이터를 split하는 함수

def split(dataset, labels, column):

    data_subsets = []

    label_subsets = []

    counts = list(set([data[column] for data in dataset])) # count는 유니크한 카테고리들

    for k in counts: # k: ['2', '4', 'more'] 각각

        new_data_subset = []

        new_label_subset = []

        for i in range(len(dataset)):

            if dataset[i][column] == k: # k에 해당하는 인스턴스들로 split

                new_data_subset.append(dataset[i])

                new_label_subset.append(labels[i])

        data_subsets.append(new_data_subset)

        label_subsets.append(new_label_subset)

    return data_subsets, label_subsets

# split 함수를 호출해봅니다.

split_data, split_labels = split(cars, car_labels, 3)

3. 반환된 변수들을 살펴봅니다.

split_data

[[['med', 'low', '3', '4', 'med', 'med'],

  ['med', 'low', '4', '4', 'med', 'low'],

  ['low', 'low', '2', '4', 'big', 'med']],

 [['med', 'vhigh', '4', 'more', 'small', 'high'],

  ['med', 'med', '2', 'more', 'big', 'high'],

  ['med', 'med', '2', 'more', 'med', 'med']],

 [['high', 'med', '3', '2', 'med', 'low'], 

  ['med', 'low', '5more', '2', 'big', 'med'],

  ['vhigh', 'vhigh', '2', '2', 'med', 'low'],

  ['high', 'med', '4', '2', 'big', 'low']]]

len(split_data)

3

 

4. split_labels를 사용하여 index 3에 대해 스플릿한 information gain을 찾아봅니다.

# index 3으로 데이터를 분할하였을 때 정보증가량을 출력해봅니다.

weighted_information_gain(car_labels, split_labels)

0.30666666666666675

 

5. 위의 정보증가량을 찾는 과정을 모든 feature에 대해서 해봅니다.

# 데이터에 있는 모든 feature들에 대하여 `split()` 함수와 `information_gain()` 함수를 호출하여 어떠한 feature이 가장 많은 information gain을 만들어 내는지 알아봅니다.

for i in range(0, 6):

  split_data, split_labels = split(cars, car_labels, i)

  print(weighted_information_gain(car_labels, split_labels))

0.2733333333333334

0.040000000000000036

0.10666666666666669

0.30666666666666675

0.15000000000000002

0.29000000000000004

---

재귀 트리 만들기 (Recursive Tree Building)

데이터를 분할하였을 때 정보증가량이 가장 높은 feature을 찾을 수 있습니다.

이 방법을 반복하는 재귀 알고리즘을 통하여 트리를 구성할 수 있습니다. 데이터의 모든 instance에서 시작하여 데이터를 분할할 가장 좋은 feature을 찾고, 그 feature에 대해서 데이터를 나눈 후에 생성된 부분집합에 대해서 재귀적으로 위의 순서를 되풀이합니다.

정보증가량이 일어나지 않는 feature을 찾을 때까지 재귀를 반복합니다. 다른 말로, 우리는 더이상 불순도가 없는 부분집합을 만드는 분할이 존재하지 않을 때 결정 트리의 끝마디를 생성합니다. 이 끝마디는 전체 데이터에서 분류된 instance의 class을 담고 있습니다.

 

# 위의 함수들을 종합하여 가장 적합한 분할 feature을 찾는 함수를 작성합니다.

def find_best_split(dataset, labels):

  best_gain = 0

  best_feature = 0

  for feature in range(len(dataset[0])):

    data_subsets, label_subsets = split(dataset, labels, feature)

    gain = weighted_information_gain(labels, label_subsets)

    if gain > best_gain:

      best_gain, best_feature = gain, feature

  return best_gain, best_feature

1. 위 함수를 cars와 car_labels에 대해 호출합니다.

best_gain, best_feature = find_best_split(cars, car_labels)

best_feature

3

best_gain

0.30666666666666675

 

2. data와 labels를 파라미터로 받는 build_tree()라는 함수를 선언하겠습니다. 이 함수는 재귀적으로 트리를 구성합니다.

def build_tree(data, labels):

  best_gain, best_feature = find_best_split(data, labels)

  if best_gain == 0:

    return Counter(labels) # 끝 노드 labels 출력

  data_subsets, label_subsets = split(data, labels, best_feature)

  branches = []

  for i in range(len(data_subsets)):

    branch = build_tree(data_subsets[i], label_subsets[i])

    branches.append(branch)

  return branches

3. 이제 만들어진 build_tree 함수를 테스트해보겠습니다. 주어진 print_tree 함수로 트리를 시각화해봅니다.

def print_tree(node, spacing=""):

    """World's most elegant tree printing function."""

    question_dict = {0: "Buying Price", 1:"Price of maintenance",

                                      2:"Number of doors", 3:"Person Capacity",

                                      4:"Size of luggage boot", 5:"Estimated Saftey"}

    # Base case: 끝노드에 도달함

    if isinstance(node, Counter):

        print (spacing + str(node))

        return

    print (spacing + "Splitting")

    # 분할 지점에서 각 브랜치에 대해 재귀적으로 print_tree 함수를 호출합니다.

    for i in range(len(node)):

        print (spacing + '--> Branch ' + str(i)+':')

        print_tree(node[i], spacing + "  ")

#  `build_tree` 함수와 `print_tree` 함수를 출력해봅니다.

tree = build_tree(cars, car_labels)

print_tree(tree)

Splitting

--> Branch 0:

   Splitting

   --> Branch 0:

      Counter({'unacc': 1})

   --> Branch 1:

      Counter({'acc': 1})

   --> Branch 2:

      Counter({'good': 1})

--> Branch 1:

   Splitting -->

   Branch 0:

      Counter({'acc': 1})

   --> Branch 1:

      Counter({'acc': 1})

   --> Branch 2:

      Counter({'vgood': 1})

   --> Branch 2:

      Counter({'unacc': 4})

---

scikit-learn으로 구현하는 결정트리

이번 활동에서는 scikit-learn 라이브러리를 사용하여 결정트리를 구현해보겠습니다.

먼저, 데이터부터 알아보겠습니다.

scikit-learn에서 제공되는 make_moons 데이터를 사용합니다.

 

1. 아래에서 데이터를 시각화해봅니다.

import matplotlib.pyplot as plt

import seaborn as sns

from sklearn.datasets import make_moons

X, y = make_moons(noise=0.324, random_state=42, n_samples=250)

sns.scatterplot(x=X[:, 0], y=X[:, 1],

                hue=y, marker="o", s=25,

                edgecolor="k", legend=False).set_title("Moon Data")

plt.show()

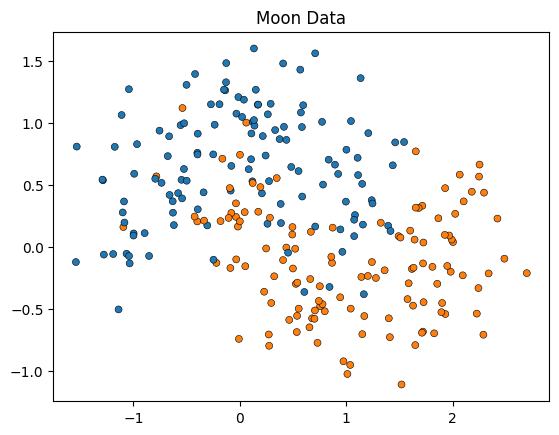
2. scikit-learn 패키지로 결정트리를 구현해보겠습니다.

DecisionTreeClassifier 분류기를 사용합니다. https://scikit-learn.org/stable/modules/generated/sklearn.tree.DecisionTreeClassifier.html?highlight=decisiontreeclassifier#sklearn.tree.DecisionTreeClassifier 

sklearn.tree.DecisionTreeClassifier

from sklearn.tree import DecisionTreeClassifier

dt = DecisionTreeClassifier()

3. 데이터에 .fit() 메소드를 호출함으로써 트리를 데이터에 훈련시킵니다.

dt.fit(X, y)

4. 정확도를 확인해봅니다.

dt.score(X, y)

1.0

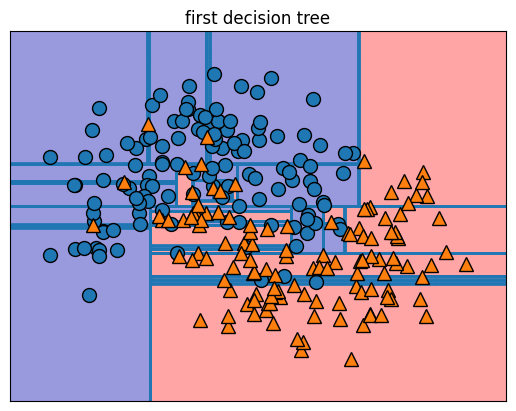
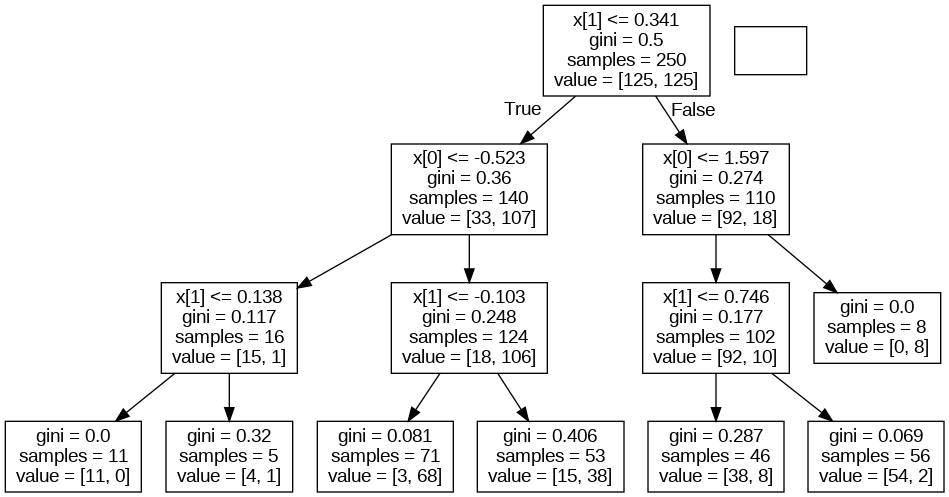
5. 완성된 결정트리를 시각화해봅니다.

# 아래 코드는 classifier 결정트리를 시각화해줍니다.

from sklearn.tree import export_graphviz # drawing graphs specified in DOT language scripts

from six import StringIO

from IPython.display import Image  

import pydotplus

dot_data = StringIO()

export_graphviz(dt, out_file=dot_data)

graph = pydotplus.graph_from_dot_data(dot_data.getvalue())

graph.write_png('/tree.png')

Image(graph.create_png())

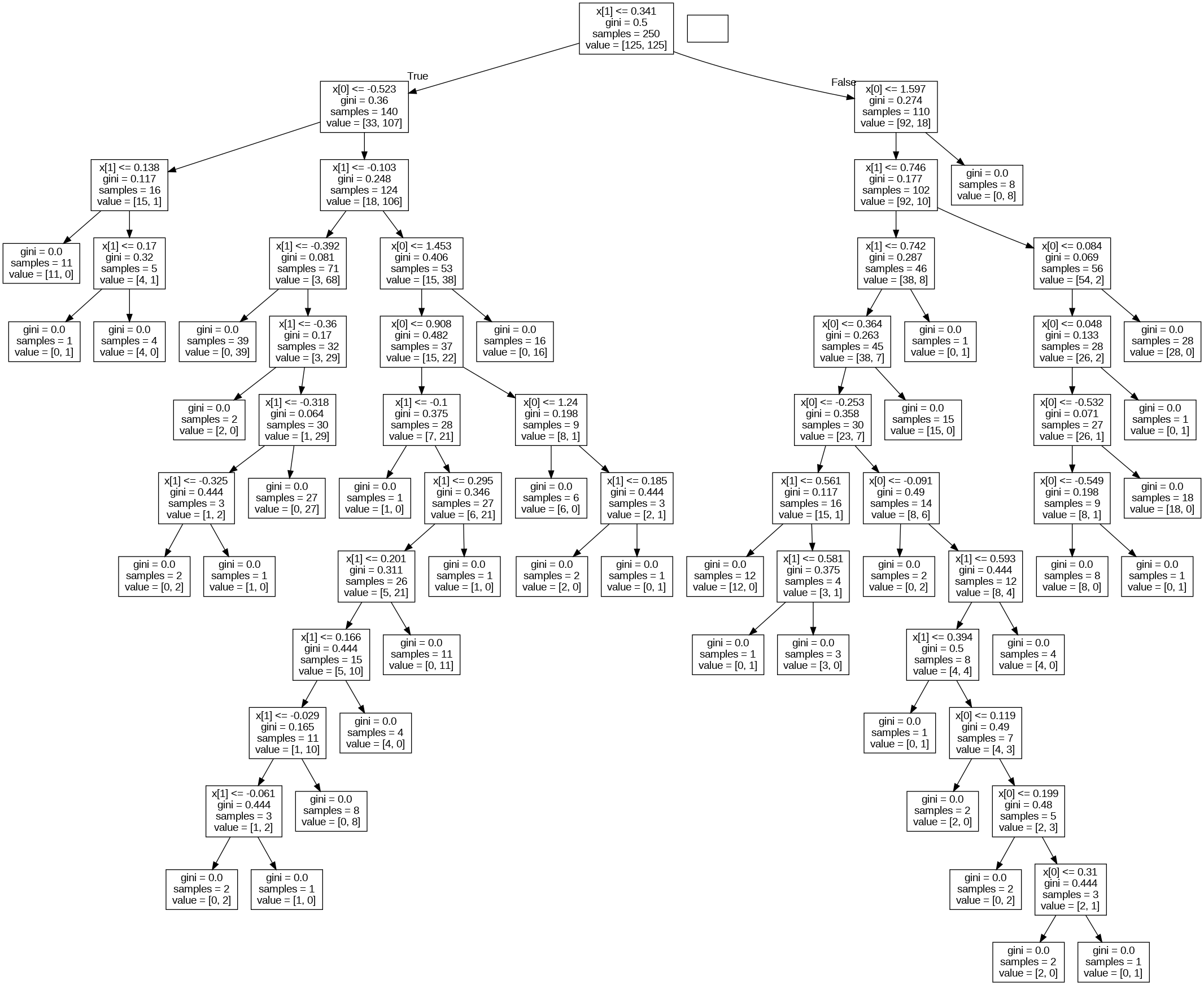
6. 결정 경계 또한 시각화 해봅니다.

from mglearn import plot_interactive_tree

ax = plot_interactive_tree.plot_tree_partition(X, y, dt)

ax.set_title("first decision tree") #제목

---

결정 트리 가지치기 (pruning)

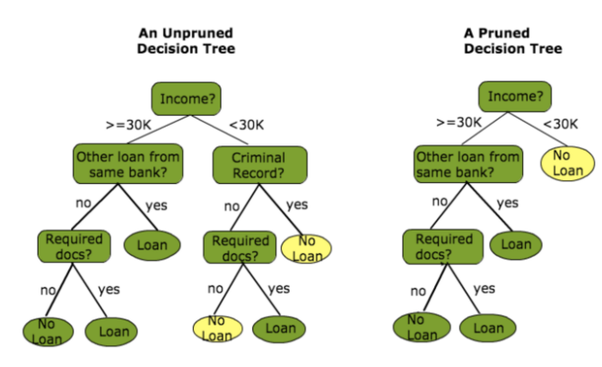
가지치기란 최대트리로 형성된 결정트리의 특정 노드 밑의 하부 트리를 제거하여 일반화 성능을 높히는 것을 의미합니다. 모든 끝노드의 불순도가 0인 트리를 full tree라고 하는데, 이 경우에는 분할이 너무 많이 과적합의 위험이 발생합니다. 과적합은 학습 데이터에 과하게 학습하여 실제 데이터에 오차가 증가하는 현상입니다. 이를 방지하기 위해서 적절한 수준에서 끝노드를 결합해주는 기법을 가지치기(pruning)이라고 합니다.

이 활동에서는 scikit-learn으로 간단한 수준의 가지치기를 구현해보겠습니다.

 

1. 새로운 결정트리를 생성합니다. 이번에는 깊이를 지정해줍니다.

pruned_dt = DecisionTreeClassifier(max_depth = 3)

pruned_dt.fit(X, y)

print(pruned_dt.score(X, y))

0.884

 

2. 가지치기된 트리를 시각화 해봅니다.

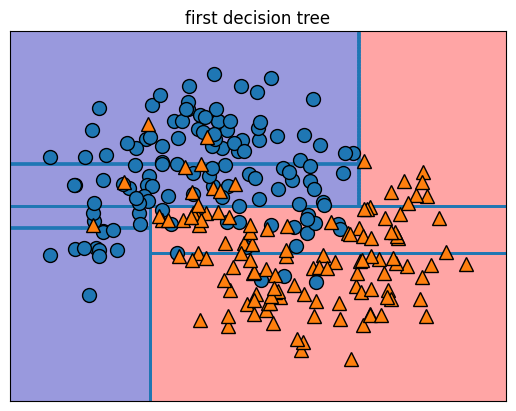
이렇게 끝노드의 개수를 지정해주면 트리가 데이터에 더욱 잘 일반화됩니다.

dot_data = StringIO()

export_graphviz(pruned_dt, out_file=dot_data)

graph = pydotplus.graph_from_dot_data(dot_data.getvalue())

graph.write_png('/tree.png')

Image(graph.create_png())

3. 결정 경계 또한 시각화해 비교해봅니다.